2021国考行测数量备考:最值问题之数列构造
在行测考试中,数量关系里最值问题的难度是相当来说中等偏下的,所以在考试的时候,遇到最值问题可以尝试去做。最值问题就是考察考生的极端思想,一般会出现“最大”、“最小”、“最多”、“最少”这样的表述,最值问题中数列构造类的题特征最为明显,下面来看看数列构造类题目的特征以及解题方法。
首先,数列构造类的题题目特征很明显,这也是比较好判别题型的原因,常出现的有两种特征:
①“最多(少)……最多(少)”时,比如:最多的……最少;最少的……最多;最少的……最少;最多的……最多,这些表述都是数列构造类的特征。
②“排名第几的……最多(少)”时,比如:排名第一的……最少;第二名的……最多,这个是第二种出现的题目特征。
题目特征掌握后可以快速的判断题型,找到相应的解题方法,数列构造类的题解题方法明确,可分为以下三步:
第一步:定位——以问题中的前半部分定位,找的时候主要看特征的第一个词“最多(少)……”和“排名第几……”将其设为未知数x。
第二步:构造——看题目中一共将整体分成几份,构造时要注意特征中后半部分的“最多(少)”,以从左到右是从多到少的固定顺序构造出几份。
第三步:求和——将构造出来的每个部分相加,就等于总数。
最后会得到一个方程,将方程求解,即可选择正确选项。
【例1】有100人参加五项活动,参加人数最多的活动的人数不超过参加人数最少活动人数的两倍,问参加人数最少的活动最少有多少人参加?
A. 10 B. 11 C. 12 D. 13 E. 14 F. 15 G. 16 H. 17
正确答案: C
【解析】第一步,本题考查最值问题,属于数列构造。
第二步,设人数最少的是x人参加,它最少意味着其他项目最多,可列表如下:
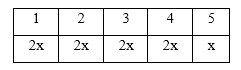
五项活动的人数为9x=100,解得x≈11.1,即最少有12人参加。
因此,选择C选项。
【例2】某连锁企业在10个城市共有100家专卖店,每个城市的专卖店数量都不同。如果专卖店数量排名第5多的城市有12家专卖店,那么专卖店数量排名最后的城市,最多有几家专卖店?
A. 2 B. 3 C. 4 D. 5
正确答案: C
【解析】第一步,本题考查最值问题中的数列构造,用构造法解题。
第二步,设排名最后的城市有x家专卖店,要使排名最后的城市最多,则其他城市专卖店数尽可能的少,根据每个城市专卖店的数量都不同进行构造可得:

第三步,根据共有100家专卖店,可列方程16+15+14+13+12+(x+4)+(x+3)+(x+2)+(x+1)+x=100,解得x=4。
因此,选择C选项。
【例3】某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多,问行政部门分得的毕业生人数至少为多少名?
A. 10 B. 11 C. 12 D. 13
正确答案: B
【解析】第一步,本题考查数最值问题中的数列构造,用构造法解题。
第二步,设行政部门人数为x,若要行政部门人数至少,则其他部门人数尽量多。行政部门比其他部门都多,可得其他部门人数最多均为(x-1),根据共招聘了65名毕业生可列方程:x+6(x-1)=65,解得x=10+。即行政部门分得的毕业生人数至少为11名。
因此,选择B选项。
最后,在做数列构造类的题的时候,要注意常见陷阱,也就是易错的地方:(1)有无各项一样,没说就可以一样;(2)有无并列情况,没说就可以并列;(3)结果小数取整,问小取大,问大取小。这样就可以掌握最值问题中数列构造类的题目了。
图图推荐:
终极冲刺密卷:http://sn.huatu.com/zt/2021gkccmj/
国考起航备考大礼包:http://sn.huatu.com/zt/2021gkcfpl/
国考模考预约:http://sn.huatu.com/2020/1106/1069174.html
历年入面分数线:http://sn.huatu.com/2018/0824/839859.html
历年国考试题:http://sn.huatu.com/guojia/shiti/

——相关阅读——
考试资讯:2021陕西省考公告发布时间|公告| 职位表下载|笔试大纲| 报考条件|招考汇总
图图力荐:2021陕西省考寒假作业| 备考大礼包| 万人模考大奖赛
省考备考:图书网课| 爆款推荐|行测备考|申论备考| 白皮书下载|资料包|笔试课程
历年信息:历年职位查询|历年入面分数线| 历年试题及题型分布|历年考情
华图在线APP--全年300+模考|30W+题库|2000+道申论智能批改|看视频 刷考题
以上是 2021国考行测数量备考:最值问题之数列构造 的全部内容,更多资讯请继续查看:陕西人事考试网、陕西公务员考试网。
(编辑:siqian)


贴心公众号客服

贴心微信客服

陕西华图教育官方微信